Advertisements
Advertisements
प्रश्न
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
पर्याय
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
उत्तर
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
Explanation:
Circumference = 176 cm
Circumference = 2πr ...(where 'r' is the radius of circle)
⇒ 176 = `2xx22/7xx"r"`
⇒ 176 × 7 = 2 × 22 × r
⇒ 1232 = 44r
⇒ `1232/44` = r
⇒ r = 28
∴ The radius of the circle = 28 cm
APPEARS IN
संबंधित प्रश्न
true or false
The degree measure of an arc is the complement of the central angle containing the arc.
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

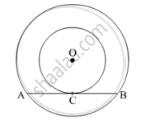
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
