Advertisements
Advertisements
प्रश्न
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
पर्याय
60 cm2
65 cm2
30 cm2
32.5 cm2
उत्तर
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is 60 cm2.
Explanation:
Firstly, draw a circle of radius 5 cm with centre O.
P is a point at a distance of 13 cm from O.
A pair of tangents PQ and PR are drawn.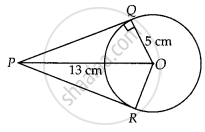
Thus, quadrilateral PQOR is formed.
∵ OQ ⊥ QP ...[Since, QP is a tangent line]
In right angled ∆PQO,
OP2 = OQ2 + QP2
⇒ 132 = 52 + QP2
⇒ QP2 = 169 – 25 = 144
⇒ QP = 12 cm
Now, area of ∆OQP
= `1/2 xx "QP" xx "QO"`
= `1/2 xx 12 xx 5`
= 30 cm2
∴ Area of quadrilateral PQOR
= 2 × ar ∆OQP
= 2 × 30
= 60 cm2
APPEARS IN
संबंधित प्रश्न
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
In the given circle with diameter AB, find the value of x.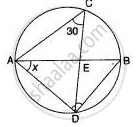
Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
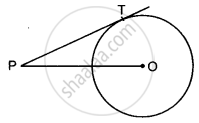
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______
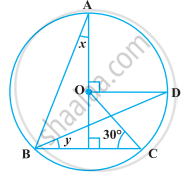
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
