Question

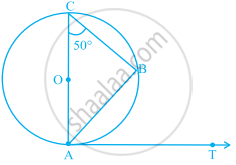
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.

पर्याय

• 65°

• 60°

• 50°

• 40°

Answer 1

In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to 50°.

Explanation:

In figure, AOC is a diameter of the circle.

We know that, diameter subtends an angle 90° at the circle.

So, ∠ABC = 90°

In ΔACB,

∠A + ∠B + ∠C = 180°  ...[Since, sum of all angles of a triangle is 180°]

⇒ ∠A + 90° + 50° = 180°

⇒ ∠A + 140° = 180°

⇒ ∠A = 180° – 140° = 40°

∠A or ∠OAB = 40°

Now, AT is the tangent to the circle at point A.

So, OA is perpendicular to AT.

∴ ∠OAT = 90°   ...[From figure]

⇒ ∠OAB + ∠BAT = 90°

On putting ∠OAB = 40°, we get

⇒ ∠BAT = 90° – 40° = 50°

Hence, the value of ∠BAT is 50°.