Advertisements
Advertisements
प्रश्न
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

उत्तर
Chords AC and DE intersect internally at point B.
∴ ∠ABE = `1/2` [m(arc AE) + m(arc DC)]
∴ 108° = `1/2` [95° + m(arc DC)]
∴ 108° × 2 = 95° + m(arc DC)
∴ 95° + m(arc DC) = 216°
∴ m(arc DC) = 216° − 95°
∴ m(arc DC) = 121°
संबंधित प्रश्न
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
Fill in the blanks:
A circle divides the plane, on which it lies, in __________ parts.
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
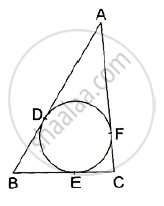
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
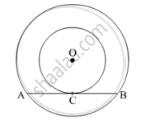
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Use the figure given below to fill in the blank:
EF is a ______ of the circle.

If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

