Advertisements
Advertisements
Question
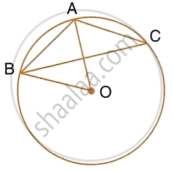
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

Solution
Chords AC and DE intersect internally at point B.
∴ ∠ABE = `1/2` [m(arc AE) + m(arc DC)]
∴ 108° = `1/2` [95° + m(arc DC)]
∴ 108° × 2 = 95° + m(arc DC)
∴ 95° + m(arc DC) = 216°
∴ m(arc DC) = 216° − 95°
∴ m(arc DC) = 121°
RELATED QUESTIONS
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

In the given figure, PQ is a chord of length 8cm of a circle of radius 5cm. The tangents at P and Q intersect at a point T. Find the length TP

If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
Prove that two different circles cannot intersect each other at more than two points.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.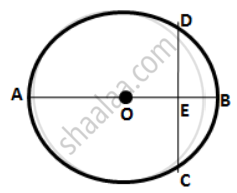
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
Find the radius of the circle
Diameter = 76 cm
In the figure, O is the centre of a circle, AB is a chord, and AT is the tangent at A. If ∠AOB = 100°, then ∠BAT is equal to ______

If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
From the figure, identify two points in the interior.

A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
