Advertisements
Advertisements
Question
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
Solution
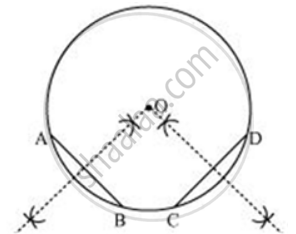
To draw the center of a given circle :
1. Draw the circle.
2. Take any two different chords AB and CD of this circle and draw perpendicular bisector of these chords.
3. let these perpendicular bisectors meet at point O.
So, O will be the center of the given circle.
APPEARS IN
RELATED QUESTIONS
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
In Fig. 1, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then the length of each tangent is:
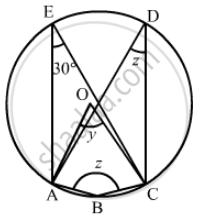
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
