Advertisements
Advertisements
Question
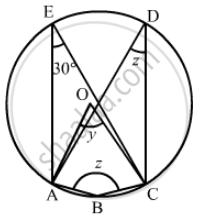
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
Solution
It is given that, O is the centre of the circle and `angle AEC = 30°`
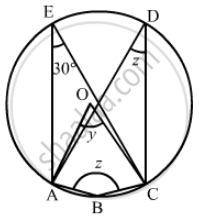
We have to find the value of x, y and z.
Since, angle in the same segment are equal
So `angle AEC = angle ADC = 30°`
And z = 30°
As angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Since `angle AOC = 2 angle ADC`
Then,
y = 2z
= 2 × 30°
= 60°
Since, the sum of opposite pair of angles of a cyclic quadrilateral is 180°.
z + x = 180°
x = 180° − 30°
= 150°
Hence,
x = 150°, y = 60° and z = 30°
APPEARS IN
RELATED QUESTIONS
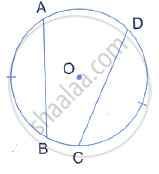
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

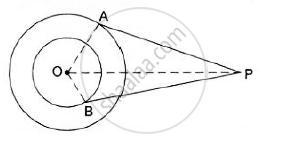
In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
The ______________ is the longest chord of a circle
Find the diameter of the circle
Radius = 10 cm
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
