Advertisements
Advertisements
प्रश्न
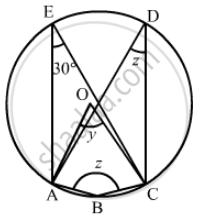
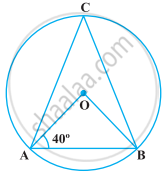
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
उत्तर
It is given that, O is the centre of the circle and `angle AEC = 30°`
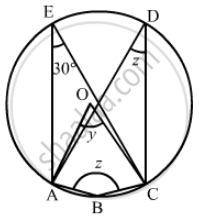
We have to find the value of x, y and z.
Since, angle in the same segment are equal
So `angle AEC = angle ADC = 30°`
And z = 30°
As angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Since `angle AOC = 2 angle ADC`
Then,
y = 2z
= 2 × 30°
= 60°
Since, the sum of opposite pair of angles of a cyclic quadrilateral is 180°.
z + x = 180°
x = 180° − 30°
= 150°
Hence,
x = 150°, y = 60° and z = 30°
APPEARS IN
संबंधित प्रश्न
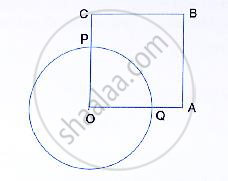
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
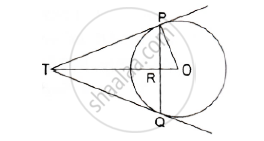
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
Use the figure given below to fill in the blank:
________ is a radius of the circle.
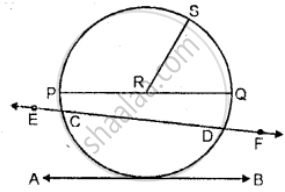
Use the figure given below to fill in the blank:
If the length of RS is 5 cm, the length of PQ = _______

In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is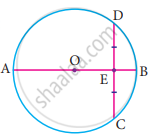
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
