Advertisements
Advertisements
प्रश्न
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is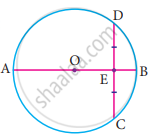
विकल्प
8 cm
4 cm
6 cm
10 cm
उत्तर
10 cm
Explanation;
Hint: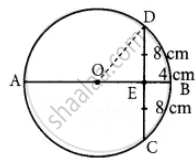
Let the radius OD be x.
OE = OB – BE
= x – 4 ...(OB radius of the circle)
In the ΔOED,
OD2 = OE2 + ED2
x2 = (x – 4)2 + 82
x2 = x2 + 16 – 8x + 64
8x = 80
x = `80/8`
= 10 cm
Radius of the circle = 10 cm.
APPEARS IN
संबंधित प्रश्न
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
All the radii of a circle are _______________
Find the diameter of the circle
Radius = 10 cm
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
