Advertisements
Advertisements
प्रश्न
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is
पर्याय
8 cm
4 cm
6 cm
10 cm
उत्तर
10 cm
Explanation;
Hint: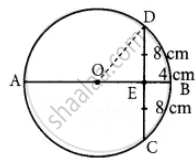
Let the radius OD be x.
OE = OB – BE
= x – 4 ...(OB radius of the circle)
In the ΔOED,
OD2 = OE2 + ED2
x2 = (x – 4)2 + 82
x2 = x2 + 16 – 8x + 64
8x = 80
x = `80/8`
= 10 cm
Radius of the circle = 10 cm.
APPEARS IN
संबंधित प्रश्न
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
A part of circumference of a circle is called as _______
A line segment with its end points on the circle is called a ______________
Find the diameter of the circle
Radius = 8 cm
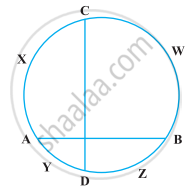
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.
Draw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate
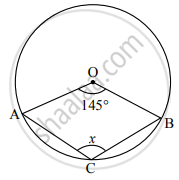
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.