Advertisements
Advertisements
प्रश्न
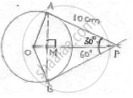
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
उत्तर
AP = 10 cm ∠APB = 60°
Represented in the figure
We know that
A line drawn from center to point from where external tangents are drawn divides or
bisects the angle made by tangents at that point ∠APO = ∠OPB =`1/2`× 60° = 30°
The chord AB will be bisected perpendicularly
∴ AB = 2AM
In ΔAMP,
sin 30° =`"𝑜𝑝𝑝.𝑠𝑖𝑑𝑒"/"ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒"="(AM)/(AP)`
AM = AP sin 30°
=`(AP)/2 =10/2`= 5𝑐𝑚
AP = 2 AM = 10 cm ---- Method (i)
In ΔAMP, ∠AMP = 90°, ∠APM = 30°
∠AMP + ∠APM + ∠MAP = 180°
90° + 30° + ∠MAP = 180°
∠MAP = 180°
In ΔPAB, ∠MAP = ∠BAP = 60°, ∠APB = 60°
We also get, ∠PBA = 60°
∴ΔPAB is equilateral triangle
AB = AP = 10 cm. -----Method (ii)
APPEARS IN
संबंधित प्रश्न
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

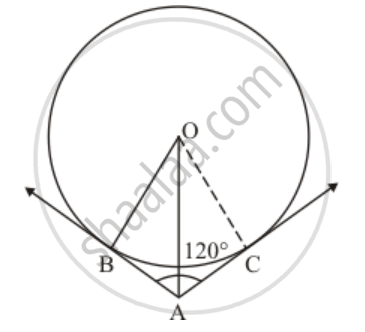
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
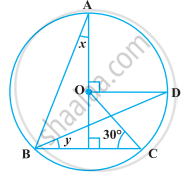
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.