Advertisements
Advertisements
प्रश्न
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
उत्तर
AP = 10 cm ∠APB = 60°
Represented in the figure
We know that
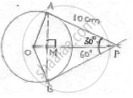
A line drawn from center to point from where external tangents are drawn divides or
bisects the angle made by tangents at that point ∠APO = ∠OPB =`1/2`× 60° = 30°
The chord AB will be bisected perpendicularly
∴ AB = 2AM
In ΔAMP,
sin 30° =`"𝑜𝑝𝑝.𝑠𝑖𝑑𝑒"/"ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒"="(AM)/(AP)`
AM = AP sin 30°
=`(AP)/2 =10/2`= 5𝑐𝑚
AP = 2 AM = 10 cm ---- Method (i)
In ΔAMP, ∠AMP = 90°, ∠APM = 30°
∠AMP + ∠APM + ∠MAP = 180°
90° + 30° + ∠MAP = 180°
∠MAP = 180°
In ΔPAB, ∠MAP = ∠BAP = 60°, ∠APB = 60°
We also get, ∠PBA = 60°
∴ΔPAB is equilateral triangle
AB = AP = 10 cm. -----Method (ii)
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
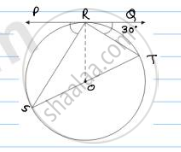
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

The greatest chord of a circle is called its
A part of circumference of a circle is called as _______
In figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70° and (arc RS) = 80°, find
(i) m(arc PR)
(ii) m(arc QS)
(iii) m(arc QSR)
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
Say true or false:
Two diameters of a circle will necessarily intersect.
