Advertisements
Advertisements
प्रश्न
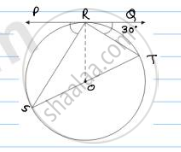
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
उत्तर
Given ∠TRQ = 30°.
At point R, OR ⊥ RQ.
∠ORQ = 90°
⇒ ∠TRQ + ∠ORT = 90°
⇒ ∠ORT = 90° − 30° = 60°
ST is diameter, ∠SRT = 90° [∵ Angle in semicircle = 90°]
∠ORT + ∠ SRO = 90°
∠SRO + ∠PRS = 90°
∠PRS = 90° − 30° = 60°
APPEARS IN
संबंधित प्रश्न
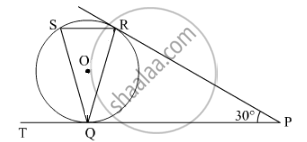
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
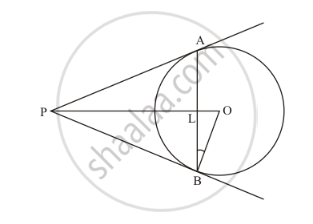
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
Draw circle with the radii given below.
2 cm
AD is a diameter of a circle and AB is a chord If AD = 30 cm and AB = 24 cm then the distance of AB from the centre of the circle is
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.