Advertisements
Advertisements
प्रश्न
Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at center.
उत्तर
Consider circle with center ‘O’ and has two parallel tangents through A & B at ends of
diameter.
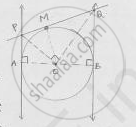
Let tangents through M intersects the tangents parallel at P and Q required to prove is that ∠POQ = 90°.
From fig. it is clear that ABQP is a quadrilateral
∠A + ∠B = 90° + 90° = 180° [At point of contact tangent & radius are perpendicular]
∠A + ∠B + ∠P + ∠Q = 360° [Angle sum property]
∠P + ∠Q = 360°−180° = 180° …..(i)
At P & Q ∠APO = ∠OPQ =1/2∠𝑃
∠BQO = ∠PQO =`1/2`∠𝑄 in (i)
2∠OPQ + 2 ∠PQO = 180°
∠OPQ + ∠PQO = 90° …. (ii)
In ΔOPQ, ∠OPQ + ∠PQO + ∠POQ = 180° [Angle sum property]
90° + ∠POQ = 180° [from (ii)]
∠POQ = 180° − 90° = 90°
∴ ∠POQ = 90°
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.
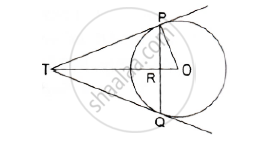
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
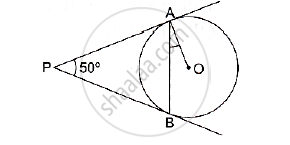
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

The circle which passes through all the vertices of a triangle is called ______.
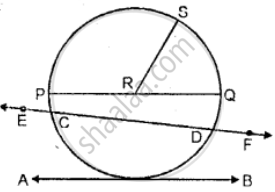
Use the figure given below to fill in the blank:
______ is a chord of the circle.
Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
A line segment which joins any two points on a circle is a ___________
