Advertisements
Advertisements
प्रश्न
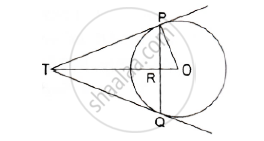
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
उत्तर
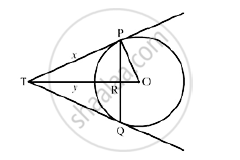
Let TR = y and TP= x
We know that the perpendicular drawn from the center to me chord bisects It.
∴ PR + RQ
Now, PR + RQ = 4.8
⇒ PR + PR = 4.8
⇒ PR = 2.4
Now, in right triangle POR
By Using Pythagoras theorem, we have
`PO^2 = OR^2 + PR^2`
`⇒3^2 = OR^2+(2.4)^2`
`⇒OR^2 =3.24`
⇒ OR = 1.8
Now, in right triangle TPR
By Using Pythagoras theorem, we have
`TP^2 = TR^2 + PR^2`
` ⇒ x^2 = y^2 +(2.4)^2`
`⇒ x^2 = y^2 + 5.76` ............(1)
Again, In right triangle TPQ
By Using Pythagoras theorem, we have
`TO^2= TP^2 + PO^2`
`⇒ (y +1.8)^2 = x^2 +3^2`
`⇒ y^2 +3.6y + 3.24 = x^2 +9`
`⇒ y^2 + 3.6y = x^2 +5.76` ...... (2)
Solving (1) and (2), we get
x = 4cm and y = 3.2cm
∴TP = 4cm
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
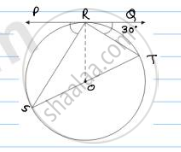
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
One chord of a circle is known to be 10 cm. The radius of this circle must be
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?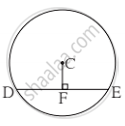
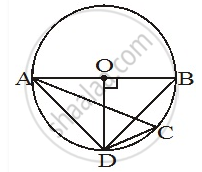
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
Say true or false:
The centre of a circle is always in its interior.
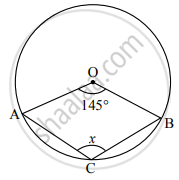
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.