Advertisements
Advertisements
प्रश्न
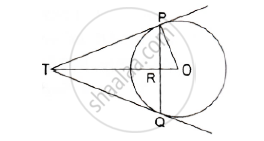
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
उत्तर
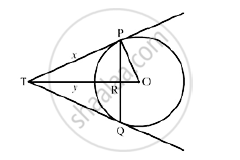
Let TR = y and TP= x
We know that the perpendicular drawn from the center to me chord bisects It.
∴ PR + RQ
Now, PR + RQ = 4.8
⇒ PR + PR = 4.8
⇒ PR = 2.4
Now, in right triangle POR
By Using Pythagoras theorem, we have
`PO^2 = OR^2 + PR^2`
`⇒3^2 = OR^2+(2.4)^2`
`⇒OR^2 =3.24`
⇒ OR = 1.8
Now, in right triangle TPR
By Using Pythagoras theorem, we have
`TP^2 = TR^2 + PR^2`
` ⇒ x^2 = y^2 +(2.4)^2`
`⇒ x^2 = y^2 + 5.76` ............(1)
Again, In right triangle TPQ
By Using Pythagoras theorem, we have
`TO^2= TP^2 + PO^2`
`⇒ (y +1.8)^2 = x^2 +3^2`
`⇒ y^2 +3.6y + 3.24 = x^2 +9`
`⇒ y^2 + 3.6y = x^2 +5.76` ...... (2)
Solving (1) and (2), we get
x = 4cm and y = 3.2cm
∴TP = 4cm
APPEARS IN
संबंधित प्रश्न
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
Use the figure given below to fill in the blank:
AB is a ______ of the circle.

Draw a circle of radius 6 cm. In the circle, draw a chord AB = 6 cm.
(i) If O is the center of the circle, join OA and OB.
(ii) Assign a special name to ∆AOB
(iii) Write the measure of angle AOB.
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.
From the figure, identify a sector.

