Advertisements
Advertisements
प्रश्न
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
पर्याय
True
False
उत्तर
This statement is False.
Explanation:
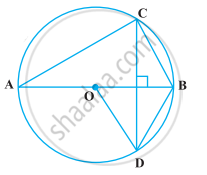
Consider the given figure.
In which we have a circle with centre O and AB a chord with ∠AOB = 60°
Since, tangent to any point on the circle is perpendicular to the radius through point of contact,
We get,
OA ⊥ AC and OB ⊥ CB
∠OBC = ∠OAC = 90° ...[Equation (1)]
Using angle sum property of quadrilateral in Quadrilateral AOBC,
We get,
∠OBC + ∠OAC + ∠AOB + ∠ACB = 360°
90° + 90° + 60° + ∠ACB = 360°
∠ACB = 120°
Hence, the angle between two tangents is 120°.
APPEARS IN
संबंधित प्रश्न
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

ture or false v
The degree measure of a semi-circle is 180°.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
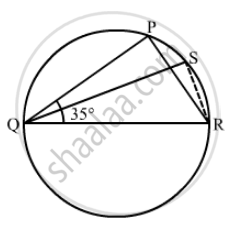
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
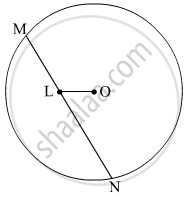
Find the radius of the circle
Diameter = 30 cm
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.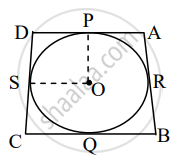
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.