Advertisements
Advertisements
प्रश्न
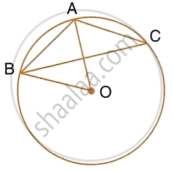
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
उत्तर
i. Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴ `∠ACB = 1/2∠AOB`
Since AB is the side of a regular hexagon,
∠AOB = 60°
ii. `∠AOB = 60^circ => ∠ACB = 1/2 xx 60^circ = 30^circ`
iii. Since AC is the side of a regular octagon,
`∠AOC = 360^circ/8 = 45^circ`
Again, Arc AC subtends ∠AOC at the center and ∠ABC at the remaining part of the circle.
`=> ∠ABC = 1/2 ∠AOC`
`=> ∠ABC = 45^circ/2 = 22.5^circ`
APPEARS IN
संबंधित प्रश्न
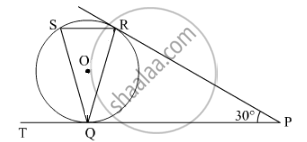
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
From a point P, two tangents PA and PB are drawn to a circle with center O. If OP =
diameter of the circle shows that ΔAPB is equilateral.
ture or false v
The degree measure of a semi-circle is 180°.
The circle which passes through all the vertices of a triangle is called ______.
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
From the figure, identify a segment.

What is the area of a semi-circle of diameter ‘d’?
