Advertisements
Advertisements
प्रश्न
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
उत्तर

Given: Chord AB || tangent XY
AB = `16sqrt(3)` units
PQ is radius of the circle.
PC = CQ
To find: Radius of the circle, i.e., l(PQ)
Construction: Draw seg PB.
In given figure, ∠PQY = 90° ......(i) [Tangent theorem]
Chord AB || line XY .....[Given]
∴ ∠PCB ≅ ∠PQY .....[Corresponding angles]
∴ ∠PCB = 90° .....(ii) [From (i)]
Now CB = `1/2` AB
∴ CB = `1/2 xx 16sqrt(3)` .....`[("A perpendicular drawn from the"),("centre of a circle on its chord"),("bisects the chord")]`
CB = `8sqrt(3)` units .....(iii)
Let the radius of the circle be x units .....(iv)
∴ PQ = x
∴ `"PC" = 1/2 "PQ"` ........[PC = CQ, P–C–Q]
∴ `"PC" = 1/2 x` .......(v)
In ∆PCB,
∠PCB = 90° .....[From (ii)]
∴ PB2 = PC2 + CB2 .....[Pythagoras theorem]
∴ x2 = `(1/2 x)^2 + (8sqrt(3))^2` .....[From (iii), (iv) and (v)]
∴ x2 = `x^2/4 + 64 xx 3`
∴ 4x2 = `(x^2)/4 + 192`
∴ `(4x^2 – x^2)/4` = 192
∴ `(3x^2)/4` = 192
∴ x2 = `192/3 xx 4`
∴ x2 = 256
∴ `sqrt(x^2)` = `sqrt256`
∴ x = 16 units ......[Taking square root of both sides]
∴ The radius of the circle is 16 units.
APPEARS IN
संबंधित प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

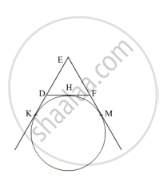
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
AD is a diameter of a circle and AB is a chord If AD = 30 cm and AB = 24 cm then the distance of AB from the centre of the circle is
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.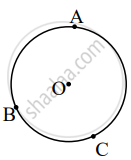
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?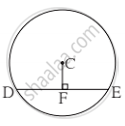
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.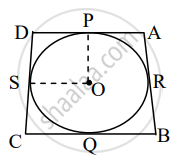
Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
Draw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.