Advertisements
Advertisements
प्रश्न
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c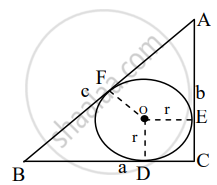
उत्तर
Proof: In given figure,
`{:("AF" = "AE"),("FB" = "BD"),("EC" = "DC"):}}` .....(i) [Tangent Segment theorem]
In ▢ODCE,
∠ECD = 90° ......[∠ACB = 90°, A–E–C, B-D–C]
`{:(∠"ODC" = 90^circ),(∠"OEC" = 90^circ):}}` ......[Tangent theorem]
∴ ∠EOD = 90° …[Ramining angle of ▢ODCE]
∴ ▢ODCE is a rectangle.
. Also, OE = OD = r ......[Radii of the same circle]
∴ ▢ODCE is a square ......`[("A Rectangle is square if it's"),("adjcent sides are congruent")]`
∴ OE = OD = CD = CE = r ......(ii) [sides of the square]
Consider R.H.S. = a + b – c
= BC + AC – AB
= (BD + DC) + (AE + EC) – (AF + FB) ......[B–D–C, A–E–C, A–F–B]
= (FB + r) + (AF + r) – (AF + FB) ......[From (i) and (ii)]
= FB + r + AF + r – AF - FB
= 2r
= L.H.S
∴ 2r = a + b – c
संबंधित प्रश्न
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
Fill in the blank:
A point whose distance from the centre of a circle is greater than its radius lies in ..................... of the circle.
Prove that two different circles cannot intersect each other at more than two points.
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

The circle which passes through all the vertices of a triangle is called ______.
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
Draw circle with the radii given below.
3 cm
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
Find the diameter of the circle
Radius = 8 cm
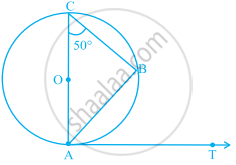
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
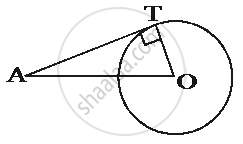
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
From the figure, identify the centre of the circle.
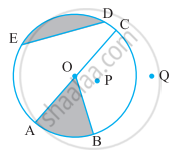
From the figure, identify a chord.

From the figure, identify two points in the interior.

Is every diameter of a circle also a chord?
