Advertisements
Advertisements
प्रश्न
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c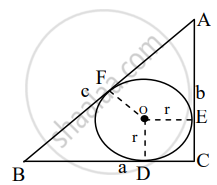
उत्तर
Proof: In given figure,
`{:("AF" = "AE"),("FB" = "BD"),("EC" = "DC"):}}` .....(i) [Tangent Segment theorem]
In ▢ODCE,
∠ECD = 90° ......[∠ACB = 90°, A–E–C, B-D–C]
`{:(∠"ODC" = 90^circ),(∠"OEC" = 90^circ):}}` ......[Tangent theorem]
∴ ∠EOD = 90° …[Ramining angle of ▢ODCE]
∴ ▢ODCE is a rectangle.
. Also, OE = OD = r ......[Radii of the same circle]
∴ ▢ODCE is a square ......`[("A Rectangle is square if it's"),("adjcent sides are congruent")]`
∴ OE = OD = CD = CE = r ......(ii) [sides of the square]
Consider R.H.S. = a + b – c
= BC + AC – AB
= (BD + DC) + (AE + EC) – (AF + FB) ......[B–D–C, A–E–C, A–F–B]
= (FB + r) + (AF + r) – (AF + FB) ......[From (i) and (ii)]
= FB + r + AF + r – AF - FB
= 2r
= L.H.S
∴ 2r = a + b – c
संबंधित प्रश्न
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

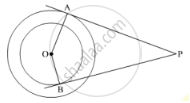
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.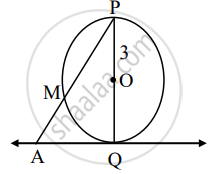
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
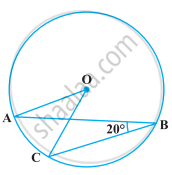
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
