Advertisements
Advertisements
प्रश्न
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
उत्तर
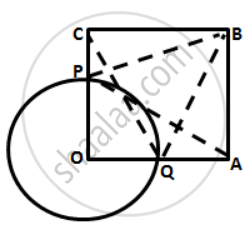
(i) In ΔOPA and ΔOQC,
OP = OQ ....[ radii of same circle ]
∠AOP = ∠COQ ... [ both 90° ]
OA = OC ... [ sides of the square ]
By Side- Angle - Side criterion of congruence.
∴ ΔOPA ≅ ΔOQC ...[ by SAS ]
(ii) Now, OP = OQ ...[ radii ]
and OC = OA ...[ sides of the square ]
∴ OC - OP = OA - OQ
⇒ CP = AQ ....(i)
In ΔBPC and ΔBQA,
BC = BA ...[ sides of the square ]
∠PCB = ∠QAB ...[ both 90° ]
PC = QA ...[ by ( i ) ]
By Side- Angle-Side criterion of congruence,
∴ ΔBPC ≅ ΔBQA ...[ by SAS ]
APPEARS IN
संबंधित प्रश्न
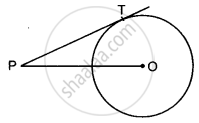
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

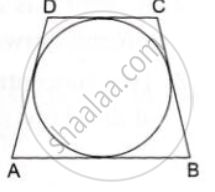
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
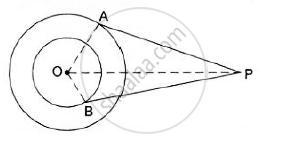
In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.
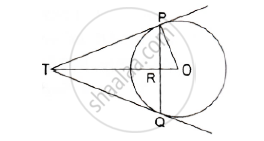
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

Draw circle with the radii given below.
3 cm
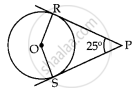
In the given figure, if ZRPS = 25°, the value of ZROS is ______
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______