Advertisements
Advertisements
Question
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA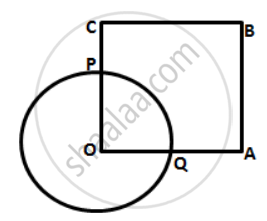
Solution
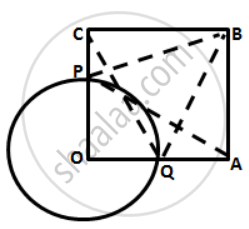
(i) In ΔOPA and ΔOQC,
OP = OQ ....[ radii of same circle ]
∠AOP = ∠COQ ... [ both 90° ]
OA = OC ... [ sides of the square ]
By Side- Angle - Side criterion of congruence.
∴ ΔOPA ≅ ΔOQC ...[ by SAS ]
(ii) Now, OP = OQ ...[ radii ]
and OC = OA ...[ sides of the square ]
∴ OC - OP = OA - OQ
⇒ CP = AQ ....(i)
In ΔBPC and ΔBQA,
BC = BA ...[ sides of the square ]
∠PCB = ∠QAB ...[ both 90° ]
PC = QA ...[ by ( i ) ]
By Side- Angle-Side criterion of congruence,
∴ ΔBPC ≅ ΔBQA ...[ by SAS ]
APPEARS IN
RELATED QUESTIONS
Prove that there is one and only one tangent at any point on the circumference of a circle.
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
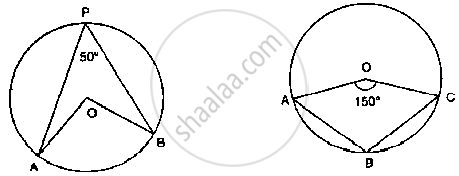
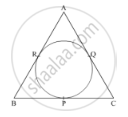
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
One chord of a circle is known to be 10 cm. The radius of this circle must be
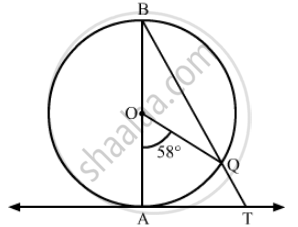
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.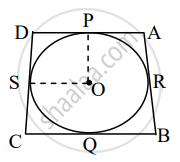
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.