Advertisements
Advertisements
Question
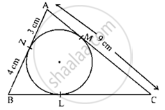
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.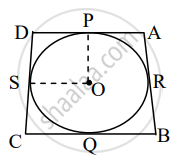
Solution
Given: AD ⊥ DC
BC = 38, QB = 27, DC = 25
To find: Radius of the circle, i.e., OP.
Solution:
BC = 38 ......[Given]
∴ BQ + QC = 38 ......[B–Q–C]
∴ 27 + QC = 38 .......[Given]
∴ QC = 38 – 27
∴ QC = 11 units ......(i)
Now, QC = SC ......[Tangent segment theorem]
∴ SC = 11 units .....(ii) [From (i)]
DC = 25 .......[Given]
∴ DS + SC = 25 ......[D–S–C]
∴ DS + 11 = 25 ......[From (ii)]
∴ DS = 25 – 11
∴ DS = 14 units ......(iii)
In ▢DSOP,
∠P = ∠S = 90° ......[Tangent theorem]
∠D = 90° ......[Given]
∴ ∠O = 90° ......[Remaning angle of ▢DSOP]
∴ ▢DSOP is a rectangle.
Also, OP = OS ......[Radii of the same circle]
∴ ▢DSOP is a square .......`[("A rectangle is square if its"),("adjacent sides are congruent")]`
∴ OS = DS = DP = PO .....(iv) [Sides of the square]
∴ OP = 14 units ......[From (iii) and (iv)]
∴ The radius of the circle is 14 units.
APPEARS IN
RELATED QUESTIONS
In the given figure, PQ is a chord of length 8cm of a circle of radius 5cm. The tangents at P and Q intersect at a point T. Find the length TP

In Fig., if AB = AC, prove that BE = EC
Fill in the blank
The angle between tangent at a point on a circle and the radius through the point is ........
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
Prove that two different circles cannot intersect each other at more than two points.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
State, if the following statement is true or false:
Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
Draw circle with the radii given below.
2 cm
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.
If O is the center of the circle in the figure alongside, then complete the table from the given information.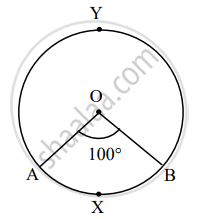
The type of arc
| Type of circular arc | Name of circular arc | Measure of circular arc |
| Minor arc | ||
| Major arc |
In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
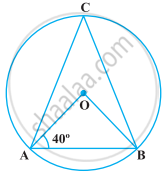
In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.
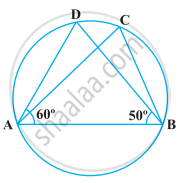
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.