Advertisements
Advertisements
Question
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
Solution
Construction: Join OA, OB, OC, OE ⊥ AB at E and OF ⊥ AC at F
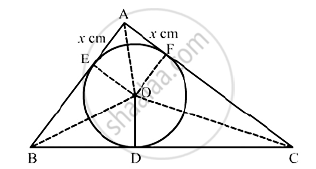
We know that tangent segments to a circle from the same external point are congruent
Now, we have
AE = AF,BD = BE = 4cmand CD = CF = 3cm
Now,
Area (ΔABC) = Area(ΔBOC)+ Area(ΔAOB) + Area(ΔAOC)
`⇒21 = 1/2 xx BC xx OD +1/2 xx AB xx OE +1/2 xx AC xx OF`
`⇒ 42 = 7 xx 2 + (4+x) xx 2 +(3+ x) xx2`
⇒ 21 = 7 + 4 + x + 3 + x
⇒ 21=14+2x
⇒ 2x =7
⇒ x= 3.5 cm
∴ AB = 4 + 3.5 = 7.5 cm and AC = 3 +3.5 = 6.5 cm
APPEARS IN
RELATED QUESTIONS
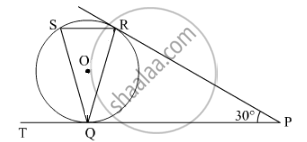
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

The circle which passes through all the vertices of a triangle is called ______.
In the given circle with diameter AB, find the value of x.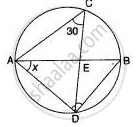
Use the figure given below to fill in the blank:
Tangent to a circle is _______.

Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is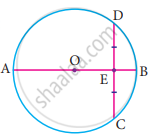
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.