Advertisements
Advertisements
Question
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
Options
True
False
Solution
True.
Let AB be a chord which is twice as long as its radius. It can be observed that in this situation, our chord will be passing through the centre of the circle. Therefore, it will be the diameter of the circle.

APPEARS IN
RELATED QUESTIONS
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
In Fig. 4, a circle inscribed in triangle ABC touches its sides AB, BC and AC at points D, E and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF.
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is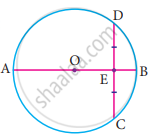
If the radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is ______
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
