Advertisements
Advertisements
Question
If the radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is ______
Options
3 cm
6 cm
9 cm
1 cm
Solution
If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is 6 cm.
Explanation:
Let O be the centre of two concentric circles C1 and C2, whose radii are r1 = 4 cm and r2 = 5 cm.
Now, we draw a chord AC of circle C2, which touches the circle C1 at B.
Also, join OB, which is perpendicular to AC.
[∵ Tangent at any point of circle is perpendicular to radius through the point of contact]
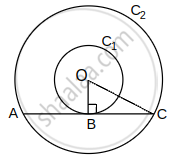
Now, in right angled ∆OBC,
By using pythagoras theorem,
OC2 = BC2 + BO2 ...[∵ (Hypotenuse)2 = (Base)2 + (Perpendicular)2]
⇒ 52 = BC2 + 42
⇒ BC2 = 25 – 16 = 9
⇒ BC = 3 cm
∴ Length of chord AC = 2BC = 2 × 3 = 6 cm
APPEARS IN
RELATED QUESTIONS
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
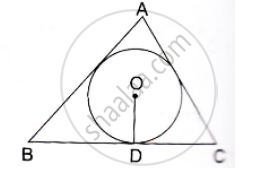
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
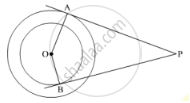
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
One chord of a circle is known to be 10 cm. The radius of this circle must be
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.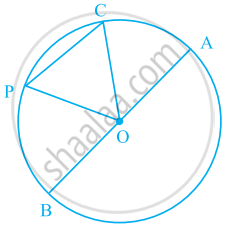
Is every diameter of a circle also a chord?
