Advertisements
Advertisements
प्रश्न
If the radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is ______
विकल्प
3 cm
6 cm
9 cm
1 cm
उत्तर
If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is 6 cm.
Explanation:
Let O be the centre of two concentric circles C1 and C2, whose radii are r1 = 4 cm and r2 = 5 cm.
Now, we draw a chord AC of circle C2, which touches the circle C1 at B.
Also, join OB, which is perpendicular to AC.
[∵ Tangent at any point of circle is perpendicular to radius through the point of contact]
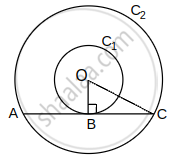
Now, in right angled ∆OBC,
By using pythagoras theorem,
OC2 = BC2 + BO2 ...[∵ (Hypotenuse)2 = (Base)2 + (Perpendicular)2]
⇒ 52 = BC2 + 42
⇒ BC2 = 25 – 16 = 9
⇒ BC = 3 cm
∴ Length of chord AC = 2BC = 2 × 3 = 6 cm
APPEARS IN
संबंधित प्रश्न
In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
Find the radius of the circle
Diameter = 76 cm
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure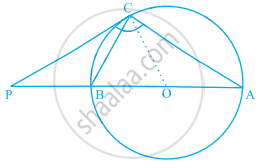
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
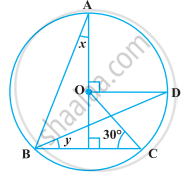
From the figure, identify a point in the exterior.

