Advertisements
Advertisements
प्रश्न
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
उत्तर
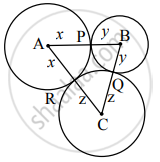
Let AP = AR = x, BP = BQ = y, CQ = CR = z .....[Radii of the same circle]
AP + BP = AB …[A – P – B]
∴ x + y = 3 …(i)
BQ + CQ = BC …[B – Q – C]
∴ y + z = 3 …(ii)
AR + CR = AC …[A – R – C]
∴ x + z = 4 …(iii)]
Adding equations (i), (ii) and (iii), we get
x + y + y + z + x + z = 3 + 3 + 4
∴ 2x + 2y + 2z = 10
∴ 2(x + y + z) = 10
∴ x + y + z = 5 …(iv)
Substituting equation (i) in equation (iv), we get 3 + z = 5
∴ z = 5 − 3
∴ z = 2 cm
Substituting equation (ii) in equation (iv), we get x + 3 = 5
∴ x = 5 − 3
∴ x = 2 cm
Substituting equation (iii) in equation (iv), we get
y + 4 = 5
∴ y = 5 − 4
∴ y = 1 cm
∴ The radii of circles with centres A, B, C are 2 cm, 1 cm and 2 cm respectively.
APPEARS IN
संबंधित प्रश्न
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
Prove that the tangents at the extremities of any chord make equal angles with the chord.
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
Write True or False. Give reason for your answer.
Sector is the region between the chord and its corresponding arc.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie.
Use the figure given below to fill in the blank:
Tangent to a circle is _______.

A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______
The length of tangent from an external point on a circle is always greater than the radius of the circle.
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
In the given figure, O is the centre of the circle. Name a chord, which is not the diameter of the circle.
Is every diameter of a circle also a chord?
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
