Advertisements
Advertisements
प्रश्न
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
उत्तर
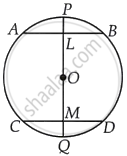
Given: AB and CD are two chords of a circle whose centre is O and PQ is a diameter bisecting the chord AB and CD at L and M, respectively and the diameter PQ passes through the centre O of the circle.
To prove: AB || CD
Proof: Since, L is the mid-point of AB.
∴ OL ⊥ AB ...[Since, the line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord]
⇒ ∠ALO = 90° ...(i)
Similarly, OM ⊥ CD
∴ ∠OMD = 90° ...(ii)
From equations (i) and (ii),
∠ALO = ∠OMD = 90°
But, these are alternating angles.
So, AB || CD
Hence proved.
APPEARS IN
संबंधित प्रश्न
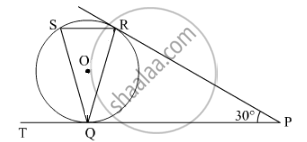
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
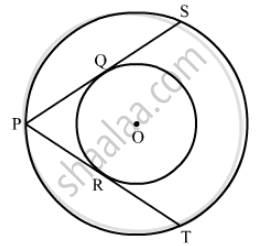
In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
In figure PA and PB are tangents from an external point P to the circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
Twice the radius is ________________
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure