Advertisements
Advertisements
प्रश्न
ABCD is such a quadrilateral that A is the centre of the circle passing through B, C and D. Prove that ∠CBD + ∠CDB = `1/2` ∠BAD
उत्तर
In a circle, ABCD is a quadrilateral having center A.
To prove ∠CBD + ∠CDB = `1/2` ∠BAD
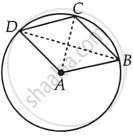
Construction: Join AC.
Proof: As we know that angle subtended by an arc at the center is double the angle subtended by it at point on the remaining part of the circle.
So, ∠CAD = 2∠CBD ...(i)
And ∠BAC = 2∠CDB ...(ii)
Now, adding equation (i) and (ii), we get
∠CAD + ∠BAC = 2(∠CBD + ∠CDB)
∠BAD = 2(∠CBD + ∠CDB)
Hence, ∠CBD + ∠CDB = `1/2` ∠BAD.
APPEARS IN
संबंधित प्रश्न
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Suppose you are given a circle. Give a construction to find its centre.
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
true or false
Line segment joining the centre to any point on the circle is a radius of the circle,
A circular park of radius 40 m is situated in a colony. Three boys Ankur, Amit and Anand are sitting at equal distance on its boundary each having a toy telephone in his hands to talk
to each other.
Prove that any three points on a circle cannot be collinear.
Choose the correct alternative:
If the points, A, B, C are non-collinear points, then how many circles can be drawn which passes through points A, B, and C?
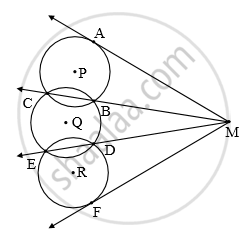
In the above figure, the circles with P, Q, and R intersect at points B, C, D, and E as shown. Lines CB and ED intersect in point M. Lines are drawn from point M to touch the circles at points A and F. Prove that MA = MF.
Through three collinear points a circle can be drawn.
Find the value of y, if the points A(3, 4), B(6, y) and C(7, 8) are collinear.
