Advertisements
Advertisements
प्रश्न
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
उत्तर
Given: O is the circumcenter of the triangle ABC and D is the midpoint of BC.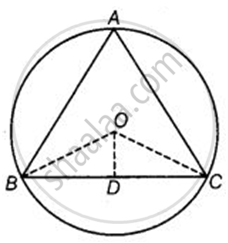
To prove: ∠BOD = ∠A
Join OB and OC.
In ΔOBD and ΔCD,
OD = OD ...(Common side)
DB = Dc ...(D is the midpoint of BC)
OB = OC ...(Both are radius of the circle)
By SSS congruence rule, ΔOBD ≅ ΔOCD.
∴ ∠BOD = ∠COD = x (say) ...(By CPCT)
Since, angle subtended by an arc at the center of the circle is twice the angle subtended by it at any other point in the remaining part of the circle, we have:
2∠BAC = ∠BOC
⇒ 2∠BAC = ∠BOD + ∠DOC
⇒ 2∠BAC = x + x
⇒ 2∠BAC = 2x
⇒ ∠BAC = x
⇒ ∠BAC = ∠BOD
Hence proved.
APPEARS IN
संबंधित प्रश्न
PA and PB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
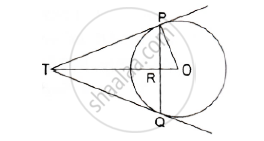
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
In the given circle with diameter AB, find the value of x.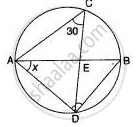
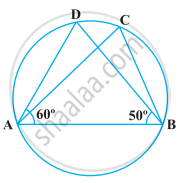
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
