Advertisements
Advertisements
प्रश्न
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
उत्तर
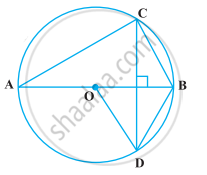
Given: ΔACB and ΔADB are two right angled triangles with common hypotenuse AB.
To prove: ∠BAC = ∠BDC
Construction: Join CD.
Proof: Let O be the mid-point of AB
Then, OA = OB = OC = OD.
Since, mid-point of the hypotenuse of a right triangle is equidistant from its verticles.
Now, draw a circle to pass through the points A, B, C and D with O as centre and radius equal to OA.
We know that, angles in the same segment of a circle are equal.
From the figure, ∠BAC and ∠BDC are angles of same segment BC.
∴ ∠BAC = ∠BDC
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
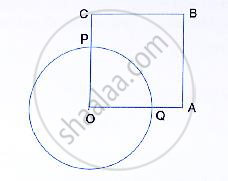
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
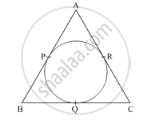
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
A part of circumference of a circle is called as _______
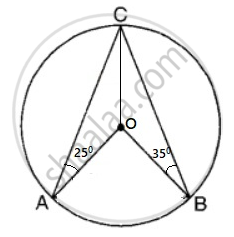
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.