Advertisements
Advertisements
प्रश्न
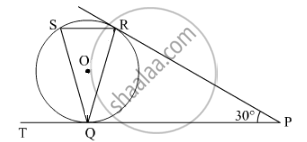
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

उत्तर
AB is the chord passing through the center
So, AB is the diameter
Since, angle in a semicircle is a right angle
∴ ∠ APB = 90°
By using alternate segment theorem
We have ∠APB = ∠PAT =30°
Now, in ΔAPB
∠BAP + ∠APB + ∠BAP = 180° (Angle sum property of triangle)
⇒ ∠BAP =180° - 90° -30° = 60°
Now, ∠BAP = ∠APT + ∠PTA (Exterior angle property)
⇒ 60° = 30° +∠PTA
⇒ ∠PTA = 60°- 30°= 30°
We know that sides opposite to equal angles are equal
∴ AP = AT
In right triangle ABP
sin ∠ABP = `(AP)/(BA)`
⇒ sin 30° = `(AT)/(BA)`
⇒ `1/2 =(AT)/(BA)`
∴ BA : AT = 2 :1
संबंधित प्रश्न
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

The circle which passes through all the vertices of a triangle is called ______.
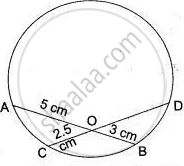
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
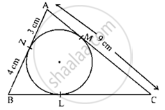
In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
