Advertisements
Advertisements
प्रश्न
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
उत्तर
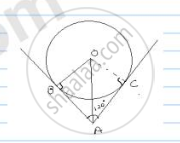
Consider Centre O for given circle
∠BAC = 120°
AB and AC are tangents
From the fig.
In ΔOBA, ∠OBA = 90° [radius perpendicular to tangent at point of contact]
∠OAB = ∠OAC =`1/2`∠𝐵𝐴𝐶 =`1/2`× 120° = 60°
[Line joining Centre to external point from where tangents are drawn bisects angle formed by tangents at that external point1]
In ΔOBA, cos 60° =`(AB)/(OA)`
`1/2=(AB)/(OA)`⇒ 𝑂𝐴 = 2𝐴𝐵
APPEARS IN
संबंधित प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
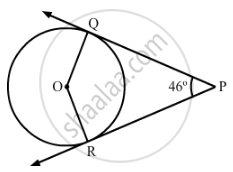
(A) 67°
(B) 134°
(C) 44°
(D) 46°
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
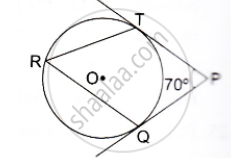
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
Draw circle with diameter: 8.4 cm
In above case, measure the length of the radius of the circle drawn.
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
The length of tangent from an external point on a circle is always greater than the radius of the circle.
