Advertisements
Advertisements
प्रश्न
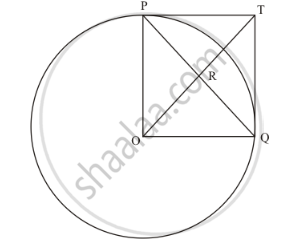
In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
उत्तर
In the given figure,
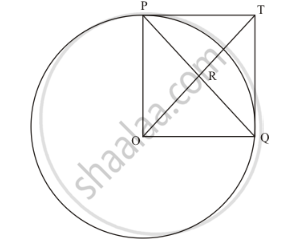
PO = OQ (Since they are the radii of the same circle)
PT = TQ (Length of the tangents from an external point to the circle will be equal)
Now considering the angles of the quadrilateral PTQO, we have,
∠POQ=90° (Given in the problem)
∠OPT=90° (The radius of the circle will be perpendicular to the tangent at the point of contact)
∠TQO=90° (The radius of the circle will be perpendicular to the tangent at the point of contact)
We know that the sum of all angles of a quadrilateral will be equal to 360°. Therefore,
∠POQ+∠TQO+∠OPT+∠PTQ=360°
90°+90°+90°+∠PTQ=360°
∠PTQ=90°
Thus we have found that all angles of the quadrilateral are equal to 90°.
Since all angles of the quadrilateral PTQO are equal to 90° and the adjacent sides are equal, this quadrilateral is a square.
We know that in a square, the diagonals will bisect each other at right angles.
Therefore, PQ and OT bisect each other at right angles.
Thus we have proved.
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
true or false
A circle is a plane figure.
true or false
A chord of a circle, which is twice as long is its radius is a diameter of the circle.
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

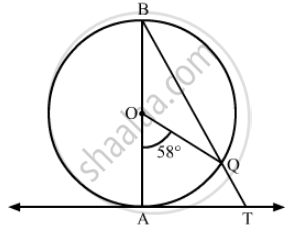
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is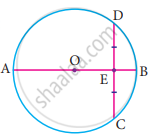
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
