Advertisements
Advertisements
Question
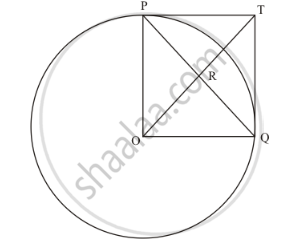
In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
Solution
In the given figure,
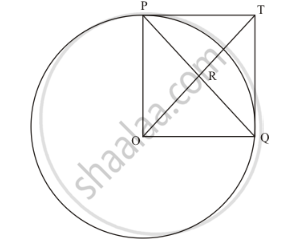
PO = OQ (Since they are the radii of the same circle)
PT = TQ (Length of the tangents from an external point to the circle will be equal)
Now considering the angles of the quadrilateral PTQO, we have,
∠POQ=90° (Given in the problem)
∠OPT=90° (The radius of the circle will be perpendicular to the tangent at the point of contact)
∠TQO=90° (The radius of the circle will be perpendicular to the tangent at the point of contact)
We know that the sum of all angles of a quadrilateral will be equal to 360°. Therefore,
∠POQ+∠TQO+∠OPT+∠PTQ=360°
90°+90°+90°+∠PTQ=360°
∠PTQ=90°
Thus we have found that all angles of the quadrilateral are equal to 90°.
Since all angles of the quadrilateral PTQO are equal to 90° and the adjacent sides are equal, this quadrilateral is a square.
We know that in a square, the diagonals will bisect each other at right angles.
Therefore, PQ and OT bisect each other at right angles.
Thus we have proved.
APPEARS IN
RELATED QUESTIONS
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
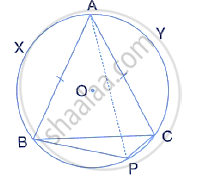
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.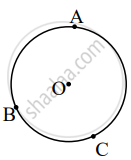
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
