Advertisements
Advertisements
Question
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

Solution
Here, OA = OB
And OA ⊥ AP,OA ⊥ BP (Since tangents drawn from an external point are perpendicular to the radius at the point of contact)
∴ ∠ OAP = 90° , ∠ OBP = 90°
∴ ∠OAP +∠ OBP = 90° + 90° = 180°
∴ ∠ AOB + ∠APB =180° (Since, ∠OAP +∠OBP +∠AOB +∠APB = 360° )
Sum of opposite angle of a quadrilateral is 180° .
Hence A, O, B and P are concyclic.
APPEARS IN
RELATED QUESTIONS
Fill in the blank
The angle between tangent at a point on a circle and the radius through the point is ........
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
If O is the centre of the circle, find the value of x in each of the following figures
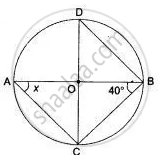
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

If O is the center of the circle in the figure alongside, then complete the table from the given information.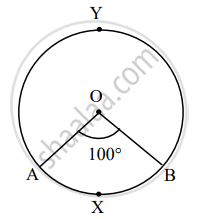
The type of arc
| Type of circular arc | Name of circular arc | Measure of circular arc |
| Minor arc | ||
| Major arc |
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.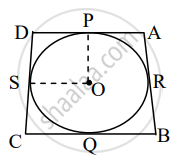
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
