Advertisements
Advertisements
प्रश्न
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

उत्तर
Here, OA = OB
And OA ⊥ AP,OA ⊥ BP (Since tangents drawn from an external point are perpendicular to the radius at the point of contact)
∴ ∠ OAP = 90° , ∠ OBP = 90°
∴ ∠OAP +∠ OBP = 90° + 90° = 180°
∴ ∠ AOB + ∠APB =180° (Since, ∠OAP +∠OBP +∠AOB +∠APB = 360° )
Sum of opposite angle of a quadrilateral is 180° .
Hence A, O, B and P are concyclic.
APPEARS IN
संबंधित प्रश्न
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
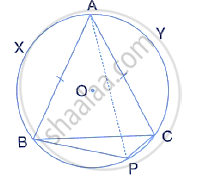
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
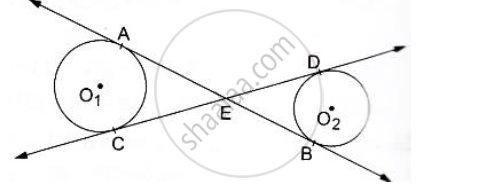
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
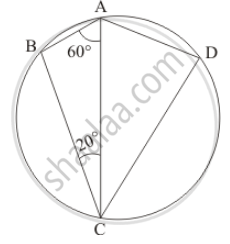
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
One chord of a circle is known to be 10 cm. The radius of this circle must be
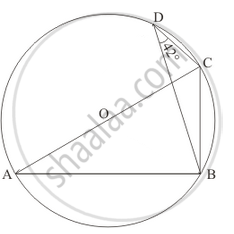
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
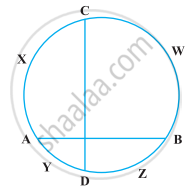
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.