Advertisements
Advertisements
प्रश्न
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
उत्तर
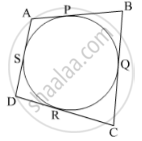
Let the sides of the quadrilateral ABCD touch the circle at points P, Q, R and S as shown in the figure.
We know that, tangents drawn from an external point to the circle are equal in length.
Therefore,
`{:[AP,=,AS],[BP,=,BQ],[CQ,=,CR],[DR,=,DS]}` ................(1)
∴AB + CD = (AP + BP) + (CR + DR)
= (AS + BQ) + (CQ + DS) [Using (1)]
= (AS + DS) + (BQ + CQ)
= AD + BC
Hence, AB + CD = AD + BC
संबंधित प्रश्न
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
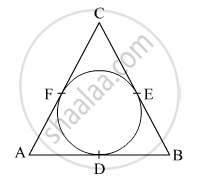
In Fig. 4, a circle inscribed in triangle ABC touches its sides AB, BC and AC at points D, E and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF.
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
The point of concurrence of all angle bisectors of a triangle is called the ______.
Find the radius of the circle
Diameter = 30 cm
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.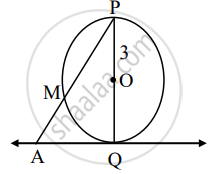
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
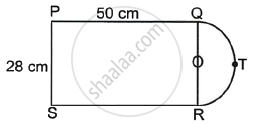
A figure is in the form of rectangle PQRS having a semi-circle on side QR as shown in the figure. Determine the area of the plot.