Advertisements
Advertisements
प्रश्न
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
उत्तर
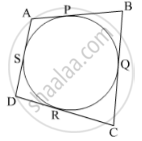
Let the sides of the quadrilateral ABCD touch the circle at points P, Q, R and S as shown in the figure.
We know that, tangents drawn from an external point to the circle are equal in length.
Therefore,
`{:[AP,=,AS],[BP,=,BQ],[CQ,=,CR],[DR,=,DS]}` ................(1)
∴AB + CD = (AP + BP) + (CR + DR)
= (AS + BQ) + (CQ + DS) [Using (1)]
= (AS + DS) + (BQ + CQ)
= AD + BC
Hence, AB + CD = AD + BC
संबंधित प्रश्न
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
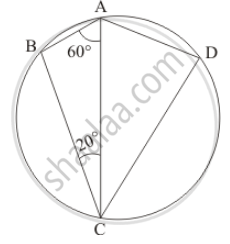
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
In the given figure, if ∠ABC = 45°, then ∠AOC =
Use the figure given below to fill in the blank:
______ is a chord of the circle.

Draw a circle of radius 4.8 cm and mark its center as P.
(i) Draw radii PA and PB such that ∠APB = 45°.
(ii) Shade the major sector of the circle
From the figure, identify a sector.

Is every diameter of a circle also a chord?
