Advertisements
Advertisements
Question
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
Solution
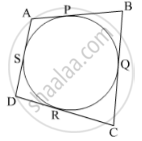
Let the sides of the quadrilateral ABCD touch the circle at points P, Q, R and S as shown in the figure.
We know that, tangents drawn from an external point to the circle are equal in length.
Therefore,
`{:[AP,=,AS],[BP,=,BQ],[CQ,=,CR],[DR,=,DS]}` ................(1)
∴AB + CD = (AP + BP) + (CR + DR)
= (AS + BQ) + (CQ + DS) [Using (1)]
= (AS + DS) + (BQ + CQ)
= AD + BC
Hence, AB + CD = AD + BC
RELATED QUESTIONS
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
Find the diameter of the circle
Radius = 8 cm
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
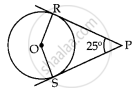
In the given figure, if ZRPS = 25°, the value of ZROS is ______
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
