Advertisements
Advertisements
Question
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

Solution
We have to prove that
AQ = `1/2` (perimeter of ΔABC)
Perimeter of ΔABC = AB + BC + CA
= AB + BP + PC + CA
= AB + BQ + CR + CA
(∵ Length of tangents from an external point to a circle are equal ∴ BP = BQ and PC = CR)
= AQ + AR ...(∵ AB + BQ = AQ and CR + CA = AR)
= AQ + AQ ...(∵ Length of tangents from an external point are equal)
= 2AQ
`\implies` AQ = `1/2` (Perimeter of ΔABC)
Hence proved.
RELATED QUESTIONS
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
Write True or False. Give reason for your answer.
Line segment joining the centre to any point on the circle is a radius of the circle.
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
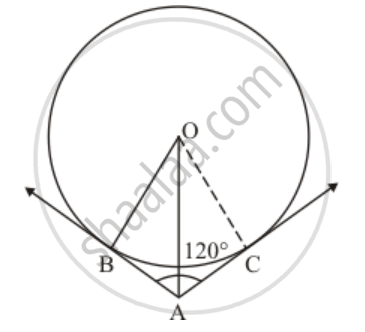
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
The ratio between the circumference and diameter of any circle is _______
The longest chord of a circle is __________
A line segment with its end points on the circle is called a ______________
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]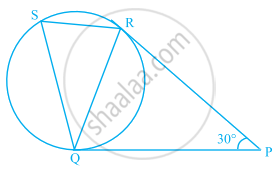
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
