Advertisements
Advertisements
Question
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]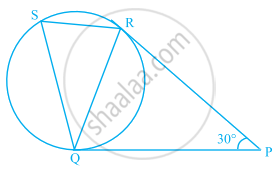
Solution
PQ and PR are two tangents drawn from an external point P.
∴ PQ = PR ...[The length of tangents drawn from an external point to a circle are equal]
⇒ ∠PQR = ∠QRP ...[Angles opposite to equal sides are equal]
Now, In ΔPQR,
∠PQR + ∠QRP + ∠RPQ = 180° ...[Sum of all interior angles of any triangle is 180°]
⇒ ∠PQR + ∠PQR + 30° = 180°
⇒ 2∠PQR = 180° – 30° = 150° ...[∵ ∠PQR = ∠QRP]
⇒ ∠PQR = `(180^circ - 30^circ)/2` = 75°
Since, SR || QP
∴ ∠SRQ = ∠RQP = 75° ...[Alternative interior angles]
Also, ∠PQR = ∠QSR = 75° ...[By alternative segment theorem]
In ΔQRS,
∠Q + ∠R + ∠S = 180° ...[Sum of all interior angles of any triangles is 180°]
⇒ ∠Q = 180° – (75° + 75°) = 30°
∴ ∠RQS = 30°
APPEARS IN
RELATED QUESTIONS
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
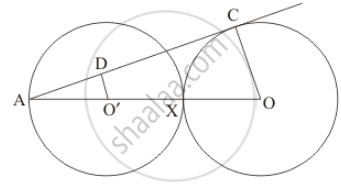
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
Use the figure given below to fill in the blank:
AB is a ______ of the circle.

If the radius of a circle is 5 cm, what will its diameter be?
Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
In figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70° and (arc RS) = 80°, find
(i) m(arc PR)
(ii) m(arc QS)
(iii) m(arc QSR)
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure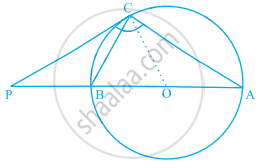
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
In the given figure, O is the centre of the circle. Name a chord, which is not the diameter of the circle.