Question

In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.

Answer 1

Join OA, OC and OB. Clearly, ∠OCA is the angle in a semi-circle.

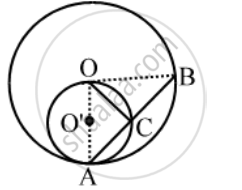
∴ ∠OCA = 90°

In right triangles OCA and OCB, we have

OA = OB = r

∠OCA = ∠OCB = 90° and OC = OC

So, by RHS criterion of congruence, we get

∆OCA ≅ ∆OCB

⇒ AC = CB