Advertisements
Advertisements
Question
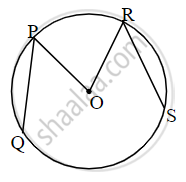
In figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70° and (arc RS) = 80°, find
(i) m(arc PR)
(ii) m(arc QS)
(iii) m(arc QSR)
Solution
(i) m(arc PR) = m∠POR ...[Definition of measure of arc]
∴ m(arc PR) = 70°
(ii)
chord PQ ≅ chord RS .....[Given]
∴ m(arc PQ) = m(arc RS) = 80° .....[Corresponding arcs of congruent chords of a circle are congruent]
Now,
m(arc QS) + m(arc PQ) + m(arc PR) + m(arc RS) = 360° ...[Measure of a circle is 360°]
∴ m(arc QS) + 80° + 70° + 80° = 360°
∴ m(arc QS) + 230° = 360°
∴ m(arc QS) = 130°
(iii) m(arc QSR) = m(arc QS) + m(arc SR) = 130° + 80° ...[Arc addition property]
m(arc QSR) = 210°
APPEARS IN
RELATED QUESTIONS
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
Draw circle with the radii given below.
2 cm
The longest chord of a circle is __________
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
Find the diameter of the circle
Radius = 8 cm
Find the radius of the circle
Diameter = 30 cm
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
