Advertisements
Advertisements
Question
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
Solution
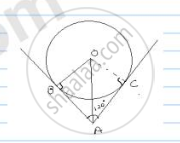
Consider Centre O for given circle
∠BAC = 120°
AB and AC are tangents
From the fig.
In ΔOBA, ∠OBA = 90° [radius perpendicular to tangent at point of contact]
∠OAB = ∠OAC =`1/2`∠𝐵𝐴𝐶 =`1/2`× 120° = 60°
[Line joining Centre to external point from where tangents are drawn bisects angle formed by tangents at that external point1]
In ΔOBA, cos 60° =`(AB)/(OA)`
`1/2=(AB)/(OA)`⇒ 𝑂𝐴 = 2𝐴𝐵
APPEARS IN
RELATED QUESTIONS
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
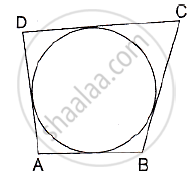
In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
Can the length of a chord of a circle be greater than its diameter ? Explain.
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
Twice the radius is ________________
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
