Advertisements
Advertisements
Question
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
Options
17 cm
15 cm
4 cm
8 cm
Solution
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is 8 cm.
Explanation:
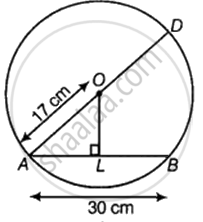
Given: Diameter of the circle = d = AD = 34 cm
∴ Radius of the circle = r = `d/2` = AO = 17 cm
Length of chord AB = 30 cm
Since the line drawn through the center of a circle to bisect a chord is perpendicular to the chord, therefore AOL is a right angled triangle with L as the bisector of AB.
∴ AL = `1/2`(AB) = 15 cm
In right angled triangle AOB, by Pythagoras theorem, we have:
(AO)2 = (OL)2 + (AL)2
⇒ (17)2 = (OL)2 + (15)2
⇒ (OL)2 = (17)2 – (15)2
⇒ (OL)2 = 289 – 225
⇒ (OL)2 = 64
Take square root on both sides:
⇒ (OL) = 8
∴ The distance of AB from the center of the circle is 8 cm.
APPEARS IN
RELATED QUESTIONS
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
true or false
Sector is the region between the chord and its corresponding arc.
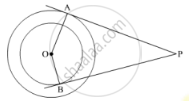
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
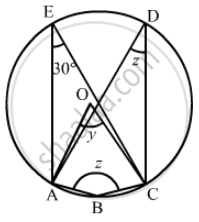
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
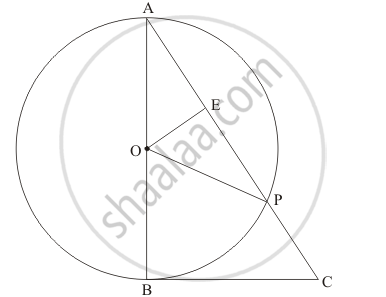
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
If O is the centre of the circle, find the value of x in each of the following figures
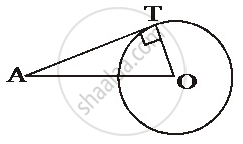
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
