Advertisements
Advertisements
प्रश्न
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
पर्याय
17 cm
15 cm
4 cm
8 cm
उत्तर
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is 8 cm.
Explanation:
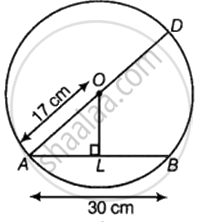
Given: Diameter of the circle = d = AD = 34 cm
∴ Radius of the circle = r =
Length of chord AB = 30 cm
Since the line drawn through the center of a circle to bisect a chord is perpendicular to the chord, therefore AOL is a right angled triangle with L as the bisector of AB.
∴ AL =
In right angled triangle AOB, by Pythagoras theorem, we have:
(AO)2 = (OL)2 + (AL)2
⇒ (17)2 = (OL)2 + (15)2
⇒ (OL)2 = (17)2 – (15)2
⇒ (OL)2 = 289 – 225
⇒ (OL)2 = 64
Take square root on both sides:
⇒ (OL) = 8
∴ The distance of AB from the center of the circle is 8 cm.
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reason for your answer.
A circle is a plane figure.
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
ture or false v
The degree measure of a semi-circle is 180°.
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
The ratio between the circumference and diameter of any circle is _______
A line segment with its end points on the circle is called a ______________
If O is the center of the circle in the figure alongside, then complete the table from the given information.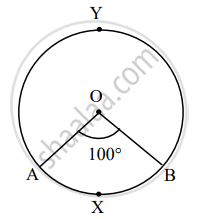
The type of arc
| Type of circular arc | Name of circular arc | Measure of circular arc |
| Minor arc | ||
| Major arc |
From the figure, identify a segment.

