Advertisements
Advertisements
प्रश्न
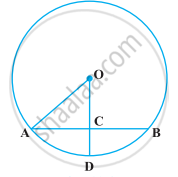
In the following figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to ______.
पर्याय
2 cm
3 cm
4 cm
5 cm
उत्तर
In the following figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to 2 cm.
Explanation:

We know that, the perpendicular from the centre of a circle to a chord bisects the chord.
AC = CB = `1/2` AB = `1/2` × 8 = 4 cm
Given OA = 5 cm
AO2 = AC2 + OC2
(5)2 = (4)2 + OC2
25 = 16 + OC2
OC2 = 25 – 16 = 9
OC = 3 cm ...[Taking positive square root, because length is always positive]
OA = OD ...[Same radius of a circle]
OD = 5 cm
CD = OD – OC
= 5 – 3
= 2 cm
APPEARS IN
संबंधित प्रश्न
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
In figure PA and PB are tangents from an external point P to the circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN
Fill in the blank
A continuous piece of a circle is ............... of the circle
Prove that two different circles cannot intersect each other at more than two points.
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
ABC is a triangle with B as right angle, AC = 5 cm and AB = 4 cm. A circle is drawn with Aas centre and AC as radius. The length of the chord of this circle passing through C and B is
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
State, if the following statement is true or false:
The diameters of a circle always pass through the same point in the circle.
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
